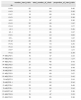
@Hutan I for example looked at the highest amount of hard rounds played in a row per player (for the first 35 rounds, excluding HV F).
For the HV you get the numbers: 2 2 2 3 5 3 12 2 2 5 2 4 2 2 5 5
For ME/CFS you get the numbers: 3 2 5 5 3 5 1 6 2 2 5 2 4 2 2
That means the mean of the highest amount of hard rounds played in a row (for the first 35 rounds) for HVs is 3.625 whilst for pwME it is 3.2, a small difference driven by HV H (the same HV H that also largely drives the end results of the study, i.e. the higher mean in choosing hard).
Of course this one statistic really captures very little or close to nothing of the dynamics of the game and how often one has to take breaks.
If you look at the highest amount of hard rounds played in a row that were won per player (for the first 35 rounds, without HV F) you would expect something more significant because pwME have a much lower percentage of completion of hard tasks. That is also precisely what you get.
For the HV you get the idential numbers: 2 2 2 3 5 3 12 2 2 5 2 4 2 2 5 5
For ME/CFS you get the numbers: 1 1 5 1 3 5 1 1 2 5 2 4 2 2
That means the mean of highest amount of hard rounds successfully completed in a row (for the first 35) rounds for HVs is 3.625 whilst for pwME it is 2.3, which is a rather large difference which already shows us quite a bit.
Now these number don't cover nearly the full "rhythm-dynamics" in which the game is played because people play hard multiple times, more often than just the one time they do their maximum and so forth. It's a bit more complicated to try to capture the full dynamics of taking "breaks". The easiest thing would be too look at the above but instead of taking just the maximum per player you take all of the occurrences, i.e. whenever someone plays hard more than once in a row you count how often that happens in a row and add all of those occurences up, that's something I haven't done yet. Alternatively one easily could look at how often do people go from easy to hard in total.
I did "come up" with a metric, that is conceptually easy, but very time consuming to implement, to capture the full dynamics of each players "breaks" which ends up giving you one final value (a number) for the amount of "breaks" for each player takes and which does account for the rhythm in which the game is played in (rather than just "playing easy=one break"). For that you plot graphs per player for the number of times people play hard/easy as the game progresses, the y axis will cature your dynamics and the x axis is just the rounds of trials. If someone plays hard multiple times in a row they get added +1 on that graph for all of those games from where they were previously standing and the first time someone goes to easy you then add -1 to their current value for that game. If they continue with easy they are given the additional value -1 (which is the difference between playing hard multiple times where you don't accumulate +1's, but for easy you do accumulate -1's, because the end metric is supposed to count the pauses/breaks you need), if they go with easy again then you go to -2, if they then play hard you go up by +1 and so forth. The metric one then uses to count the breaks per player is something mathematics call total variation and essentially measures the total height of your graph. You can then add up all total varitations of the individual players to get the mean for each group (ME/CFS and HV). You do the same thing for games in a row as well as games succesfully played in a row (with the difference here being that successes for easy count the same way as just choosing easy, since both are a break).
I'm somewhat confident this captures taking "breaks" reasonably well over the full duration of the game (but I still have to think about it properly and am not even sure about if the whole thing does what you want it to do) and gives you one number at the end of everything that also captures the dynamics of the game (I'm also fairly confident I explained it very badly and posting a graph would better explain what I mean). I think one will be able to come up with something better or even something better by just looking at the easy rounds, because these are the breaks, but I haven't really come up with something yet that also accounts for the rhythm in which the game is played. I also still have to think about whether the above thing is the right way to go about this and whether it really captures everything you want to capture and if that is even meaningful at all.
Whether that would end up giving you something valuable I currently don't know, especially because the variation in what pwME do in this trial is so high and there is no obvious "rhythm" in how the game is played rather than just different people doing completely different things.
The end idea would probably be to have some notion "how often does someone have to take breaks but yet still choose to do hard, even if he can't". But I'm not sure if any of the above means anything and I'm guessing that it doesn't, because the whole setup of the game is very unrobust.
Last edited:
